Numerical Examples of Fracture

Finite Element Analysis

Finite element analysis is a tool used in engineering to determine the physical effects a given set of boundary conditions will have on a part. Boundary conditions can be forces, temperatures, hydrostatic pressures, centrifugal pressures, torques, and displacements. Finite element analysis can be as basic as a simple FORTRAN code or as complex as some of today's high end Finite Element Analysis Software Packages (MARC). The basic theory of finite element analysis is the same regardless of the type of analysis being done. The geometry being modeled will always be divided up into smaller divisions known as elements and the elements are connected together to form the finite element mesh. Each element contains nodes which are points were the elements are mathematically connected to one another. The idea of dividing a domain up into subdomains is the basic principle of how FEA works. The basic steps which are involved in creating a finite element model are now going to be outlined as we create a plain strain model of an infinite plate, with an elliptical hole in the middle, loaded in the simple tension. This model represents one of the basic ideas of fracture mechanics, stress intensity. This problem also has an analytical solution with which we can compare our FEA results to determine the validity of our model.

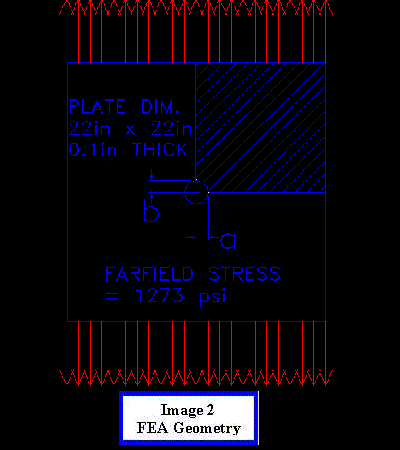The first step in creating a finite element model is to input the geometry of the part you want to model. Often the geometry being modeled will have some type of symmetry, which can be taken advantage of to save time both generating the model and solving the model. As you can see only ¼ of the geometry (the crosshatched section of Image 2) will need to be modeled to look at the stress intensity at the transverse side of the elliptical hole. After the geometry has been created the next step is to turn the surface of the plate into a mesh. For this model we will use a four-sided element with a node at each corner. A technique commonly used in FEA is mesh biasing. Mesh biasing is using smaller elements in areas where the stress gradient is the large or in areas where an extremely accurate prediction of stress is necessary. In this model we biased the mesh towards elliptical hole to produce an accurate value of the stress intensity.
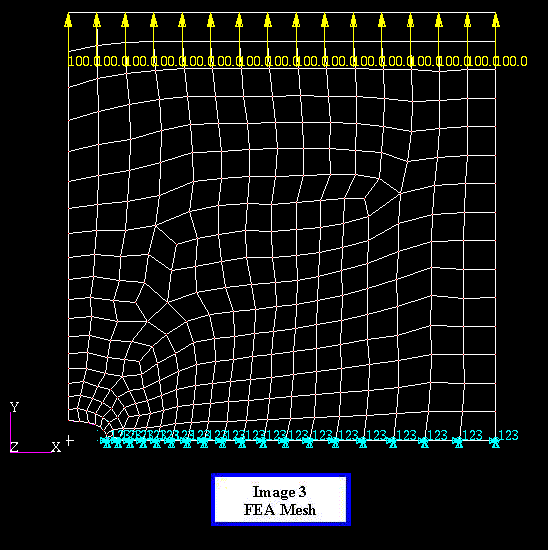Since we are only modeling part of the plate it is important that add the correct boundary conditions to simulate the same effects that would occur if the entire plate were being modeled. The only things we will need to add are displacement restraints on the bottom edge of the model perpendicular to the direction of the loading. We want to induce a Farfield Stress of 1273 psi in the plate so we will put a 100-LB tensile force on each node across the top of the plate. This completes the boundary conditions for the model.

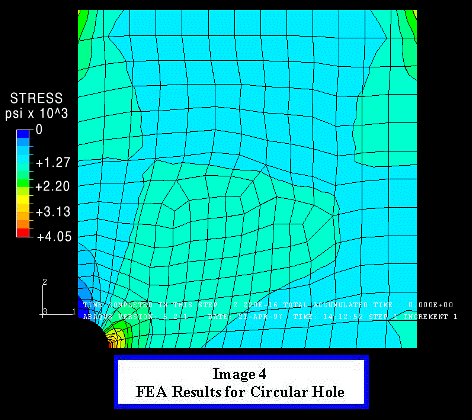Now we must define the material properties for the elements, in this model we will use the physical properties of steel, modulus of elasticity 30 *10^6 psi and poison ratio of 0.30. This completes the finite element model, now we will submit the model to a solver, ABAQUS was used for this model, which will return the geometry with the stress levels indicated by different colors.

The results of an FEA from most software packages look fairly similar to the output of the above model. The areas of highest stress are indicated by red, descending to the lowest stress levels in blue. The next task is to determine whether or not the results our model produced are accurate. In this case we can obtain an exact solution to our model using the analytical solution to the stress concentration produced by an elliptical hole in an infinite plate under simple tension, which given by the relationship:


where "a" and "b" are both parameters of the ellipse (shown in second image). In this model the ellipse was actually a circle so the stress concentration is just three times the Farfield Stress, which gives a stress concentration of 3819 psi. The FEA returned the stress concentration at the hole to be 4050 psi, which is 6% higher than the exact solution. The 6% error would be reasonable for most engineering design applications because an exact solution is not critical because a factor of safety will be added in the part design.
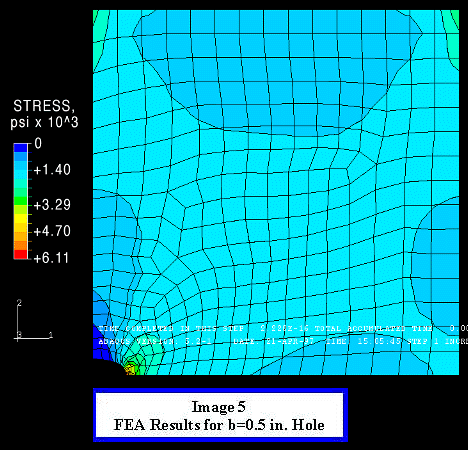Next we will examine the same plate with two smaller "b" values for the ellipse. Decreasing the "b" of the ellipse is analogous to decreasing the radius of a crack tip in crack. In the next model "b" decreases to 0.5 in. Again we have the luxury of being able to calculate an exact solution for the stress concentration, which is five times the Farfield Stress, 6365 psi. The FEA result was 6110 psi, which is 4% lower than the exact solution. Again this small error negligible, however inspecting the stress as you approach the crack tip from the right reveals a very large stress gradient across a very small number of elements. This model still produces a valid solution but we will see that when "b" is reduced to 0.25 in. the mesh size around the crack tip is too large to produce a valid solution. When "b" is reduced to 0.25 in. the analytical solution for the stress concentration becomes nine times the Farfield stress, 11457 psi. However the FEA only shows a stress concentration of 7010 psi. This large error, 38%, is due to the fact the stress gradient is so large across the elements next to the crack tip that they no longer yield valid solutions. The corrective action for this problem would be to decrease the element size around the crack tip, resulting in more elements around the crack tip. With increased exposure to FEA one would learn to question results that come from a mesh which has such a large stress gradient over a small number of elements. Thus we can see that an FEA can produces highly accurate results of stress concentration when the mesh is sized reasonably well compared to the stress gradient and the same rule holds true for any type of FEA. However in real engineering applications there will be no exact solution to the models. Engineers must depend on their knowledge and intuition to determine whether the results of an FEA are valid.

Further Reading:

Special Thanks to:

Return to Table of Contents

This page was written by Jeff Schultz.

Revised 4-24-97