Overview:
One of the most important parts of the any engineering design are the materials that involved in its construction. All materials have weaknesses and strengths and it is vital that a designer realize the limitations of certain materials. The purpose of this section of the fracture web project is to inform MSE 2034 and MSE 2044 students what principle material parameters should be taken into consideration to prevent or promote fracture. In addition, this section of the web project will desribe how these materials can be modified so that they meet necessary design criterion.

Factor of Safety and Fracture Design
All engineers must answer a fundemental question, "How safe is the design?" An equation, Se-1, is used to express the safety of a design's mechanical strength as a ratio between the applied stresses on the materials in the design, and the materials' yield or tensile strength.

Equation Se-1 [1]. the equation for the factor of safety

Usually when designing a part, a material's s_u is replaced with the material's yield strength, not tensile strength. This makes good common sense. Most airplanes, for example, can not afford to have their wings plastically deformed by stresses and still have the same flight characteristics as before. The value of the factor of safety is also dependent on the application. Fighter jets may have a factor of safety of 1.1, but industrial machinary may have a factor of safety of 3 or higher.

How will the Design Fracture?
What if a material does begin to fail or fractures? Will the people nearby have time to react? The time interval between the beginning of failure and total failure is a very important question in fracture design. There are two primary ways that a material can fail, ductile fracture, or brittle fracture. In brittle fracture, the material fails in a quick, catastrophic fashion. Ductile fracture is little more forgiving. Often there is ample time to notice crack propagation in a material that fails ductily, and fix the problem before the materials completely fails. Engineering students you are strongly encouraged to read over the topics ductile fracture and brittle fracture.

Can the Design be Tested without Destroying It?
Today's engineers now have the ability to model a design in a computer environment and apply loads to the virtual design. The standard way of doing this is with a FEA (Finite Element Analysis) program. Engineering students should take a good look at the section on FEA that was developed for this web project to get a better understanding of how computers can help improve fracture design.

Why do Things Usually Fail?
Most failures occur not because one applied load is too great, but because a small load is applied repeatedly, this kind of failure is a result of fatigue.

Geometry and Fracture Design:
Not surprisingly, a part's geometry has an impact on its mechanical performance. The geometry of a part can lead to stress to concentrations. Mechanical engineers, especially, should beware of stress concentrations when they design any part, no matter how small. No matter how strong or tough the material that the part is made of, a poorly shaped design can have catastrophic consequences. Figures Sf-1 and Sf-2 show two machined pieces. Figure Sf-1 has a sharp end that create a stress concentration. Figure Sf-2 uses a fillet instead, minimizing additional stresses on the part.

Figure Sf-1 [1]. A poor design that will create a stress concentration

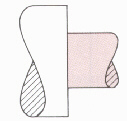
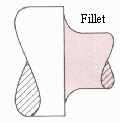
Figure Sf-2 [1]. Good design will minimize stress concentrations

To learn more about these concentrations the web project has an entire section set aside for stress concentrations.

Example Problem : Factor of Safety
A high strength piece of cabling is made from a special alloy, called Ronkrizite.
(s_t = 3500 MPa, s_y =2000 MPa). The fiber's diameter is 0.01 m. The load that will be applied to the cabling is 10⁵ N. What is the factor of safety?

Answer:
Step 1) Calculate the applied stress.
s_a = Load / Area = (10⁵ N) / ( (Pi/4) (0.01 m)2 )
s_a = 1270 MPa

Step 2) Assume that the material's yield stress, not tensile stress should be used in the factor of safety equation. A designer should always use the yield strength unless told otherwise.
F.S. = s_u / s_a
F.S. = s_y / s_a
F.S. = 2000 MPa / 1270 MPa
F.S. = 1.57

Submitted by Matt Gordon

Virginia Tech Materials Science and Engineering

http://www.eng.vt.edu/eng/materials/classes/MSE2094_NoteBook/97ClassProj/exper/gordon/www/gordon.html

Last updated: 4/27/97