 The array that is interpolated. The array must be a two-dimensional floating-point array with dimensions (n, m).
The array that is interpolated. The array must be a two-dimensional floating-point array with dimensions (n, m).x
 A floating-point array containing the x subscripts of array (see Discussion). Must satisfy the following conditions:
A floating-point array containing the x subscripts of array (see Discussion). Must satisfy the following conditions:
Standard Library function that creates an array containing values calculated using abilinear interpolation to solve for requested points interior to an input grid specified by the input array.
 The array that is interpolated. The array must be a two-dimensional floating-point array with dimensions (n, m).
The array that is interpolated. The array must be a two-dimensional floating-point array with dimensions (n, m).x
 A floating-point array containing the x subscripts of array (see Discussion). Must satisfy the following conditions:
A floating-point array containing the x subscripts of array (see Discussion). Must satisfy the following conditions:
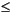 min(x)
min(x) 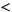 n
n 0
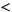 max(x)
max(x) 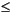 n
n
 A floating-point array containing the y subscripts of array (see Discussion). Must satisfy the following conditions:
A floating-point array containing the y subscripts of array (see Discussion). Must satisfy the following conditions:
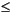 min(y)
min(y) 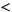 m
m 0
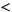 max(y)
max(y) 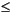 m
m
 A two-dimensional floating-point array (n, m) containing the results of the bilinear interpolation for the requested points.
A two-dimensional floating-point array (n, m) containing the results of the bilinear interpolation for the requested points.If x is of dimension i and y is of dimension j, the result has dimensions (i, j). In other words, both x and y will be converted to (i, j) dimensions. If you want the result to have dimensions (i, j), then x can be either FLTARR(i) or FLTARR(i, j). This is also true for y.
The array x/y contains the X/Y subscripts of the elements in array that are used for the interpolation:
TIP: Using two-dimensional arrays for x and y with BILINEAR in-creases the speed of the algorithm. If x and y are one-dimensional, they are converted to two-dimensional arrays before they are returned by the function. This permits them to be reused in subsequent calls to BILINEAR, thereby saving time.
array = FLTARR(3,3) array(1, 1) = 1
x = [.1, .2] y = [.1, .4, .7, .9]
PRINT, BILINEAR(array, x, y)
0.0100000 0.0200000
0.0400000 0.0800000
0.0700000 0.140000
0.0900000 0.180000
a = DIST(100) original = SHIFT(SIN(a/5)/EXP(a/50),50,50)
LOADCT, 5
TVSCL, original
b = FINDGEN(100)
PLOT, b
x = b^2 / 100.0
OPLOT, x
y = x
result = BILINEAR(original, x, y)
ERASE TVSCL, result


