DIGITAL_FILTER Function
Standard Library function that constructs finite impulse response digital
filters for signal processing.
Usage
Input Parameters
Returned Value
Keywords
Discussion
TIP: A value of 50 for gibbs is a good choice for most filters.
Sample Usage
NOTE: Two or more filters created by DIGITAL_FILTER can be combined by addition, subtraction, or averaging to create multiple filtering effects with one filter.
Example 1
av_temp = FLTARR(140)
OPENR, unit, !Data_dir + 'example_air_q.dat', /Get_lun
READF, unit, av_temp, Format='(5X,F9.4)'
FREE_LUN, unit
PLOT, av_temp
filter = DIGITAL_FILTER(0.0, 0.1, 50, 10)
filt_temp = CONVOL(av_temp, filter)
OPLOT, filt_temp, Linestyle=2
Example 2
mandril = BYTARR(512,512)
OPENR, unit, !Data_dir + 'mandril.img', /Get_lun
READU, unit, mandril
FREE_LUN, unit
WINDOW, XSize=512, YSize=512
TV, mandril
mandril = FLOAT(mandril)
filter = DIGITAL_FILTER(0.0, 0.1, 50, 10)
filt_image = CONVOL(mandril, filter)
TV, filt_image
See Also



doc@boulder.vni.com
Copyright © 1999, Visual Numerics, Inc. All rights
reserved.
 The value of the lower frequency of the filter, expressed as a fraction of the Nyquist frequency. Must be between 0 and 1.
The value of the lower frequency of the filter, expressed as a fraction of the Nyquist frequency. Must be between 0 and 1. The value of the upper frequency of the filter, expressed as a fraction of the Nyquist frequency. Must be between 0 and 1.
The value of the upper frequency of the filter, expressed as a fraction of the Nyquist frequency. Must be between 0 and 1. The size of the Gibbs Phenomenon variations. Expressed in units of -db (decibels).
The size of the Gibbs Phenomenon variations. Expressed in units of -db (decibels). The number of terms in the filter formula used. Determines the order of the filter.
The number of terms in the filter formula used. Determines the order of the filter.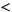 fhigh
fhigh 

