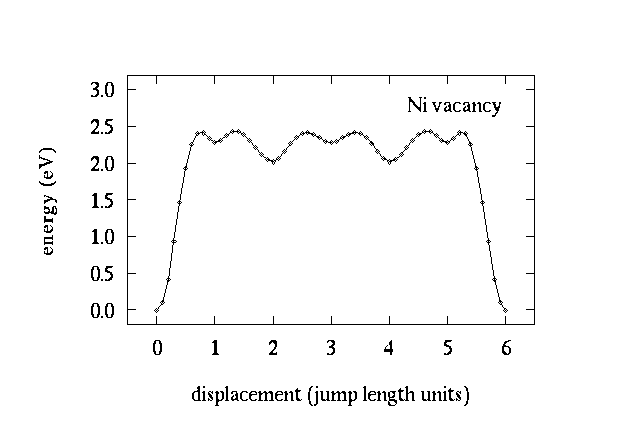
Figure 1. Six jump cycle energy barrier for one Ni vacancy in NiAl.
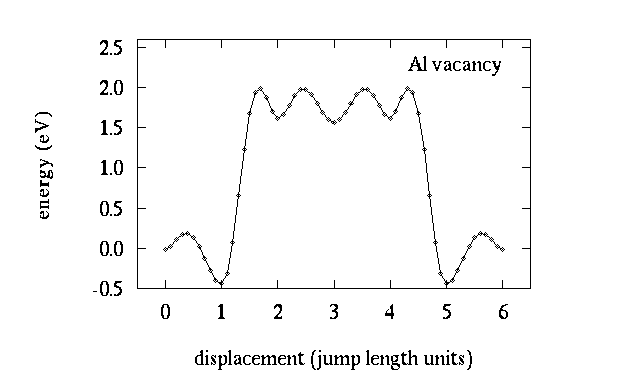
Figure 2. Six jump cycle energy barrier for one Al vacancy in NiAl

In the work described here we have used various EAM potentials
for the NiAl system. They are as follows:
Click here to see graphic information about the potentials.
We have calculated the energetics of point defects in NiAl using the various potentials mentioned above.
In all cases the antisite defects where Al occupied a Ni site is highly unfavored
(Z.Y. Xie and Diana Farkas, J. Mater. Res. 9, 875, 1994 and MRS Symp. Proc 288, 305, 1993).
The deviations of stoichiometry for Al rich alloys are actually accommodated by Ni vacancies
( Y. Mishin and D. Farkas, submitted to Phil. Mag., 1996). These calculations actually enable the
determination of the chemical potentials of Ni and Al from the thermodynamic definitions for both
Al rich and Ni rich alloys.
EAM simulations allow the study of the activation energy barriers involved in diffusion
(Y. Mishin and D. Farkas, submitted to Phil. Mag., 1996). The calculations show that self-diffusion in
NiAl is dominated by next nearest neighbor jumps.
However, the six jump mechanism is still highly competitive. It is expected that off-stoichiometry
will have a strong influence on diffusion rates, with increasing Al content increasing the diffusion rate.
Potentials Used
Point Defects
Diffusion

Figure 1. Six jump cycle energy barrier for one Ni vacancy in NiAl.

Figure 2. Six jump cycle energy barrier for one Al vacancy in NiAl
Grain Boundaries
We have computed various grain boundary structures for high angle special grain boundaries in NiAl (G. Petton and D. Farkas, Scr. Met 25, 55, 1991). A number of structures are possible for the same misorientation having very similar energies. The following figure illustrates an example structure.

Figure 3
High Al boundaries have lower cohesive energies. A comparative study with CoAl and FeAl shows the boundaries in the three compounds to be similar (B. Mutasa and D. Farkas, in IIB95, edited by A.C. Ferro, J.P. Conde and M.A. Fortes, Transtech Publications, Switzerland, page 305, 1996.
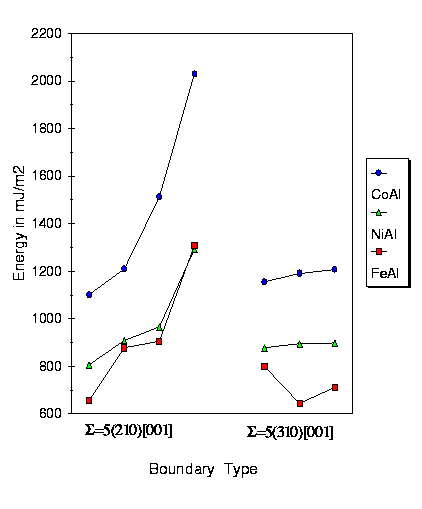
Figure 4
Dislocation Core Structure
Dislocation core structure simulations have been carried out using anisotropic elasticity as boundary conditions for the atomsitic simulations. Peierls stresses for the various dislocations were also obtained from the simulations. Screw dislocations are unstable in this material, as predicted by anisotropic elasticity theory and simulations. For edge and mixed dislocations most cores are non-planar, showing sessile behavior.
The lowest Peierls stress for non-screw dislocations was found for the mixed <100> dislocation along a <210> dislocation line with a <001> slip plane (K. Ternes, D. Farkas and Z.Y. Xie, MRS Symp. 350, 293,1994). A comparative study of this dislocation in three B2 compounds was performed (C. Vailhé and D. Farkas, MRS Proceedings, MRS Fall Meeting 1994) and (C. Vailhé, V. Shastry and D. Farkas, TMS Proceedings, TMS Materials Week, 1994, edited by W.O. Soboyejo, T.S. Srinivasan and R.O. Ritchie, page 179). Here is how dislocation cores behave for the different materials. We also studied the effects of deviations from stoichiometry on the dislcoation cores. (J.K. Ternes and D. Farkas, Phil. Mag. A 72, 1671, 1995). The Peierls stress of these dislocations increases when deviations of stoichiometry are introduced. For non-stoichiometric alloys, the non-planar dislcoation cores tend to loose the well-defined preference for spreading along certain crystallographic planes.
Our current work also concentrates on crack propagation in intermetallics. We have completed work
in Fe (V. Shastry and D. Farkas, MRS Symp. 409, 75 ,1996) and we are now simulating fracture in NiAl.
Crack Propagation

Figure 5. A crack in NiAl that has emitted [100] dislocations

Figure 6. Grain boundary fracture in NiAl. (The boundary is a symmetrical tilt sigma=5 boundary)
