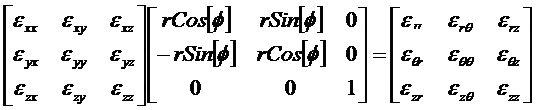ESM 4714 - Scientific Visualiztion and Data Anaylsis
Class Contract
Profs: Dr. Kriz and Jason Lockhart
3 - 17 - 2003

Background:

            The Naval Surface Warfare Center (NSWC-DD) in Dahlgren, Virginia is interested in determining the pressures created during an explosive test of a material called Deta-Sheet (DS). Similar to the explosive C-4 in terms of its stability, DS comes in quarter inch thick sheets out of which different size charges can be cut.  Below is a example of a 1.25 x1.25 in² section (9 grams) of this DS, with a RP80 detonator, used to initiate the charge. There were also tests with a 6 gram charge, a 13.3 gram charge and a 20 gram charge.

            In order to contain the blast, a 20 inch long cylinder, with one sealed end and another ported end, was constructed out of stainless steel. The modal characteristics of this cylinder were gathered using accelerometers and modeled with a Finite Element model. The next step was to confirm the model using the mode shapes and frequencies gathered from modal testing. Figure 2 below shows the testing configuration for the modal analysis.

            Once the FE model was built, we next needed to determine the locations to put strain gages that would act as our measured output, from which we could predict the pressure blast.  We choose locations that will facilitate the inverse process of this problem. Strain gages were placed around the cylinder in sets of prime numbers, 7 and 3, helping differentiate between similar modes and their orientation, and at specific node lines, thereby eliminating detection of certain modes of the cylinder. After investigating the FE model, the following locations were chosen:

1)      Halfway along the length of the cylinder – thereby eliminating any of the lower longitudinally symmetrical modes. (Sin Waves along the length)

2)      Approximately 2/3 from the bottom of the cylinder – thereby eliminating from detection some of the higher frequency mode shapes. (1.5 sine waves along the length)

            Below is a set of figures that show the FE mode shapes thru 2.5 kHz and the transfer function for hoop and longitudinal strain when the model is forced under a uniform 10.707 kPa impulse.

            Now, using strain as the output to the blast, and the cylinder as the transducer, we can predict the force generated during the blast using the Finite Element model to generate the relationship between strain and force.

Project Goal:

For this project, we are going to “visualize” the strain gathered from the surface of the cylinder, during testing. This will be a step by step process in which we will first visualize the cylinder. The next step will be to put the displacements into the visualization. Finally, the strain will be added as a color map, on the displaced cylinder.

Project Duties:

In order to do this we will take advantage of the information that is available to us. First keep in mind that all of the strain data gathered is in the form of Hoop or Longitudinal strain versus time. With a simple FFT, this time domain data can be transformed to frequency data. Next, from the FE model we can extract the mode shapes and reconstruct the FRF of the whole cylinder (This, however, is not as simple as it sounds). Then, taking the experimental data, and matching the spatial location of a strain gage to a node in the cylinder model, we can magnify all of the nodal strains for each mode of the cylinder to match that of the strain “seen” by the strain gage at the specified frequency or mode shape. Once this is done for all of the modes that we are interested in, we can compare the response predicted with these methods to the response measured at a different location measured experimentally.

It will be interesting to see the affects of:

1. Including more than just one mode in the prediction

2. Including more than just one experimentally measured strain gage  

I will be responsible for preparation of the data that will later be visualized.

1. Create a file of node numbers and locations for creation of the undeformed cylinder.

2. Create a file of node numbers and displacements for each mode that is going to be considered in the analysis.

3. Transform the Cartesian strain data per element into cylindrical coordinates, for each mode

4. Change the format of the strain output from strain per element to strain per node, for each mode.

5. Recombine the strain data for each node and each mode into a transfer function relation of strain of the amplified mode to strain at any other node considered.

6. BREATHE!!!  

Wesley will be responsible for visualizing the prepared data.

1. For each time step, create a 3-D ANSYS model of the deformed cylinder, with a color gradient representing hoop and longitudinal strain for the desired test.

2. Using the successive JPEG images from the ANSYS models at each time step, create a movie of the deforming cylinder with a changing color gradient representing strain.

Equations Used:

Modal Breakdown